miniDSP
A small C library for audio DSP
Loading...
Searching...
No Matches
Spectrogram and the STFT

This tutorial walks through the examples/spectrogram.c program, which generates a linear chirp, computes its STFT with MD_stft(), converts to dB, and writes an interactive HTML heatmap.

If you haven't already, read the Computing the Magnitude Spectrum tutorial first — it covers the DFT fundamentals that the STFT builds on.

What is the STFT?

The magnitude spectrum shows the frequency content of an entire signal. But audio signals are rarely stationary — a speech sentence, a musical phrase, or a chirp sweep all have frequency content that changes over time.

The Short-Time Fourier Transform (STFT) solves this by dividing the signal into short, overlapping frames and computing the DFT of each one. The result is a two-dimensional time-frequency representation called a spectrogram.

For frame \(f\) and frequency bin \(k\), the STFT is:

\[ X_f(k) = \sum_{n=0}^{N-1} w[n]\, x[f \cdot H + n]\, e^{-j 2\pi k n / N} \]

where:

  • \(N\) is the FFT window size (samples per frame)
  • \(H\) is the hop size (samples between successive frames)
  • \(w[n]\) is the Hanning window
  • \(x[\cdot]\) is the input signal

MD_stft() stores \(|X_f(k)|\) in a row-major matrix: mag_out[f * (N/2+1) + k].

Time-frequency resolution trade-off

Choosing \(N\) involves a fundamental trade-off:

Narrow window (small N) Wide window (large N)
Time resolution High Low
Frequency resolution Low High
Bins Few Many

A common starting point for speech and music at 16 kHz is \(N = 512\) (32 ms), which gives adequate resolution in both dimensions.

The hop size \(H\) controls frame overlap. 75% overlap ( \(H = N/4\)) is a standard choice that produces smooth spectrograms without excessive computation.

Step 1: Generate a chirp signal

A linear chirp sweeps instantaneous frequency from \(f_0\) to \(f_1\) linearly over a duration \(T\):

\[ x(t) = \sin\!\left(2\pi \left(f_0 + \frac{f_1 - f_0}{2T}\,t\right) t\right) \]

A chirp is the ideal test signal for a spectrogram because its instantaneous frequency changes over time, producing a clearly visible diagonal stripe across the time-frequency plane.

MD_chirp_linear(signal, signal_len, 1.0, chirp_f0, chirp_f1, sample_rate);
MD_chirp_linear
void MD_chirp_linear(double *output, unsigned N, double amplitude, double f_start, double f_end, double sample_rate)
Generate a linear chirp (swept sine with linearly increasing frequency).
Definition minidsp.c:617

Step 2: Compute the STFT

MD_stft_num_frames() tells you how many complete frames fit in the signal, so you can allocate the output buffer before calling MD_stft().

MD_stft(signal, signal_len, N, hop, mag_out);
MD_stft
void MD_stft(const double *signal, unsigned signal_len, unsigned N, unsigned hop, double *mag_out)
Compute the Short-Time Fourier Transform (STFT) of a real-valued signal.
Definition minidsp.c:860

MD_stft() applies the Hanning window internally, so the signal does not need to be pre-windowed. The output mag_out is a row-major matrix with num_frames rows and N/2+1 columns. Magnitudes are raw FFTW output — not normalised by \(N\).

Step 3: Convert to dB

Raw magnitudes span many orders of magnitude. A log scale compresses the dynamic range and makes both loud and quiet features visible simultaneously.

Normalise by \(N\) before taking the log so that a full-scale sine (amplitude 1) reads near 0 dB. Floor at \(10^{-6}\) to avoid \(\log(0)\).

for (unsigned i = 0; i < num_frames * num_bins; i++) {
spec_db[i] = 20.0 * log10(fmax(mag_out[i] / (double)N, 1e-6));
}

The formula 20 log \(_{10}\) is used because the input is a magnitude (amplitude), not a power.

Results

The resulting spectrogram shows the chirp as a diagonal stripe rising from 200 Hz at \(t = 0\) to 4000 Hz at \(t = 2\) s. Hover over the interactive plot to read exact time, frequency, and dB values.

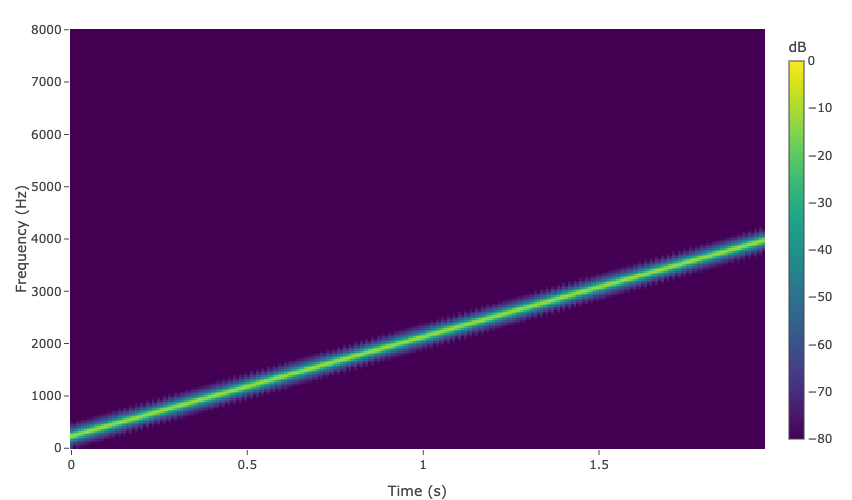
STFT spectrogram of a 200 → 4000 Hz linear chirp

Key takeaways

  • The STFT slides a windowed FFT over a signal to reveal how its frequency content evolves over time.
  • Window size \(N\) controls the time-frequency trade-off: larger \(N\) gives finer frequency resolution but coarser time resolution.
  • Hop size \(H < N\) creates overlapping frames. 75% overlap ( \(H = N/4\)) is a common default.
  • MD_stft() reuses the same cached FFT plan as MD_magnitude_spectrum() and MD_power_spectral_density(), so mixing calls with the same \(N\) incurs no extra plan-rebuild overhead.
  • Divide magnitudes by \(N\) before dB conversion so that a unit-amplitude sine reads near 0 dB.

Further reading

API reference